Deep learning 2 - Logistic Regression as a Neural Network

Neural Networks Basics

Bài viết này chúng ta sẽ tập trung vào những kiến ​​thức cơ bản về lập trình mạng nơ-ron (Neural network), đặc biệt là một số kỹ thuật quan trọng, chẳng hạn như cách xử lý các ví dụ huấn luyện m trong tính toán và cách triển khai quá trình lan truyền tiến (forward propagation) và lan truyền ngược (Backward propagation).

Logistic Regression

Logistic Regression (Hồi quy logistic) là một kỹ thuật khác được học máy mượn từ lĩnh vực thống kê.

Đây là phương pháp phù hợp cho các bài toán phân loại nhị phân (các bài toán có hai giá trị lớp). Và Logistic Regression là cách đơn giản để cho chúng ta thấy cách hoạt động neural network.

Logistic Regression Cost Function

Trong hồi quy logistic, chúng ta muốn huấn luyện các tham số w và b, chúng ta cần xác định hàm chi phí.

\[\hat{y} = \sigma(w^{T}x^{(i)}+b)\] \[\text{Trong đó: } \sigma(z^{(i)}) = \frac{1}{1 + e^{-z^{(i)}}}\] \[\text{Dữ liệu:} \{(x^{(1)}, y^{(1)}), ..., (x^{(m)}, y^{(m)})\] \[\text{Mục tiêu: } \hat{y}^{(i)} ≈ y^{(i)}\]

Nếu đây là lần đầu tiên bạn tiếp cận với Logistic Regression thì bạn có thể xem bài giảng về LR của tôi tại đây Logistic Regression lecture hoặc đọc blog này machinelearningcoban.com/2017/01/27/logisticregression, tôi tin là sau khi đọc xong bạn sẽ hiểu vẻ đẹp của Logistic Regression.

Loss Function là hàm mất mát đo sự chệnh lệch giữa y dự đoán \(\hat{y}^{i}\) và y thực tế \(y^{i}\), nói đơn giản hơn thì nó tính lỗi (chi phí) cho một ví dụ (sample) huấn luyện.

\[L(\hat{y}^{(i)}, y^{(i)}) = \frac{1}{2}(\hat{y}^{(i)} - y^{(i)})^{2}\] \[L(ŷ(i), y(i)) = -(y(i) \log(ŷ(i)) + (1 - y(i)) \log(1 - ŷ(i)))\] \[\begin{cases} L(ŷ, y) = \log(ŷ) & \text{if } y = 1 \\ L(ŷ, y) = \log(1 - ŷ) & \text{if } y = 0 \end{cases}\]

Cost function là tính toán trung bình tất cả lỗi, chi phí của cả tập huấn lệnh, và mục tiêu của chúng ta là tìm w và b để Cost function là nhỏ nhất cho tập huấn lệnh.

\[\begin{equation} J(w, b) = \frac{1}{m} \sum_{i=1}^m L(\hat{y}^{(i)}, y^{(i)}) = -\frac{1}{m} \sum_{i=1}^m [(y^{(i)} \log(\hat{y}^{(i)}) + (1 - y^{(i)})\log(1 - \hat{y}^{(i)})] \end{equation}\]

Ngắn gọn hơn:

\[J(w, b) = -\sum_{i=1}^m \log(\hat{y}^{(i)})^{y^{(i)}} (1 - \hat{y}^{(i)})^{1 - y^{(i)}}\]

Hàm mất mát (Loss function) đo lường mức độ hiệu quả của mô hình trên một ví dụ đào tạo, trong khi hàm chi phí (Cost function) đo lường mức độ hiệu quả của mô hình (cụ thể là các tham số w và b) trên toàn bộ tập huấn luyện.

Gradient Descent

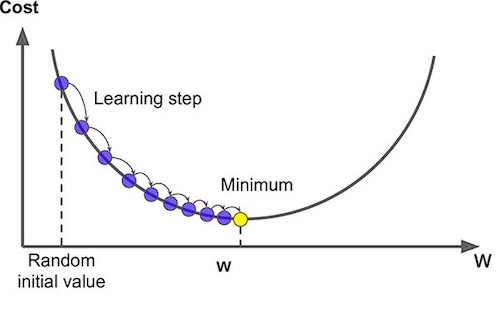
Khi chúng ta học bất kỳ khóa học nào về Machine learning hoặc Deep learning thì Gradient Descent sẽ là thứ xuất hiện phổ biến nhất, bạn nên master kỹ thuật này, Nó được sử dụng khi train model, khi mà các cost function quá phức tạp để tìm w và b tối ưu, thì Gradient Descent xuất hiện, nó có thể kết hợp với mọi thuật toán một cách dễ hiểu và dễ thực hiện.

Tôi đã có những slide và bài tập về Gradient Descent và bạn có thể xem ở đây, Ngoài ra bạn cũng có thể tham khảo ở đây: GD1, GD2

Nói ngắn gọn về ý tưởng của Gradient Descent là:

• Khởi tạo các tham số w, b ngẫu nhiên (thường thì xấp xỉ 0).
• Tính Cost and Gradient cho tập training với tham số w, b.
• Update các tham số w và b với learning rate đặt trước:

\[w_{new} = w_{old} – lr * \text{gradient_of_at}(w_{old})\]

làm tương tự với b.

• Lặp lại các bước này cho đến khi bạn đạt được giá trị tối thiểu của Cost function, từ đó bạn sẽ có được w và b tối ưu.

Derivatives (Đạo hàm)

Trong deep learning, các model là Neural network quá trình predict từ input ra output là forward propagation (lan truyền xuôi) và update các trọng số để tối ưu mô hình là backpropagation (lan truyền ngược), Đạo hàm rất quan trọng trong quá trình lan truyền ngược lúc train model, sử dụng khái niệm đồ thị tính toán và quy tắc đạo hàm chuỗi (Chain rule) để giúp việc tính toán hàng nghìn tham số trong mạng thần kinh hiệu (neural network) quả hơn sẽ được giới thiệu phía dưới.

Computation Graph (Đồ thị tính toán)

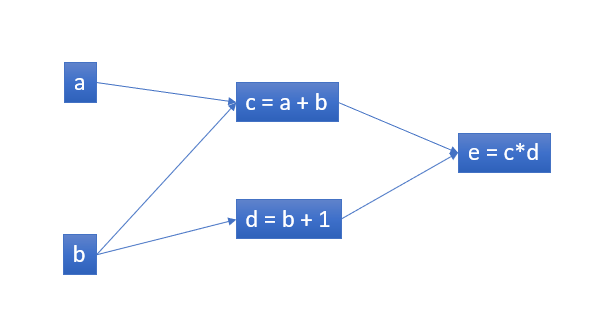
Đồ thị tính toán là một cách hay để hiểu ý tưởng tính toán của các neural network, thực chất neural network chỉ là tổ hợp của những biểu thức toán học. Ví dụ, hãy xem xét biểu thức e=(a+b)∗(b+1). Có ba phép tính: hai phép cộng và một phép nhân. Để giúp chúng ta giải quyết vấn đề này, hãy giới thiệu hai biến trung gian c và d để đầu ra của mọi hàm đều có một biến. Chúng ta hiện có:

\[c = a + b\] \[d = b + 1\] \[e = c ∗ d\]

Từ đây chúng ta có thể tạo ra một Computation Graph với các dữ liệu đầu vào là nút lá:

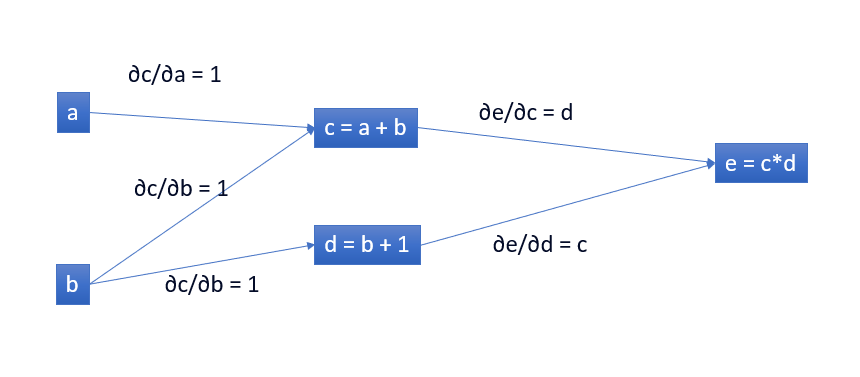
Sau đó chúng ta có thể đạo hàm với đồ thị tính toán này:

Nếu muốn hiểu đạo hàm trong neural network, thì phải hiểu đạo hàm trong một đồ thị tính toán, điều quan trọng là phải hiểu đạo hàm trên các cạnh. Nếu a ảnh hưởng trực tiếp đến c thì chúng ta muốn biết nó ảnh hưởng đến c như thế nào. Nếu a thay đổi một chút thì c thay đổi như thế nào? Chúng ta gọi đây là đạo hàm riêng của c theo a.

Ví dụ nếu ∂c/∂a = 1 tức là nếu a tăng 1 thì c tăng 1, a tăng 2 thì c tăng 2, còn nếu ∂e/∂c = d thì nếu c tăng 2 thì e tăng d*2.

Điều này rất tốt để chúng ta hiểu cách hoạt động của quy tắc Chain rule lên neural network, bạn có thể tìm hiểu thêm về quy tắc chain rule.

Chain rule

Chain rule nói rằng: Đạo hàm hàm tổng hợp = đạo hàm hàm bên ngoài * đạo hàm hàm bên trong

\[\begin{equation} f(x) = A(B(C(x))) \end{equation}\] \[\begin{equation} f'(x) = \frac{d}{dx} [A(B(C(x)))] = (A'(B(C(x))) \cdot B'(C(x))) + (A(B(C(x))) \cdot C'(x)) \end{equation}\]

Điều này giúp chúng ta đạo hàm được những hàm lồng hàm trong neural network.

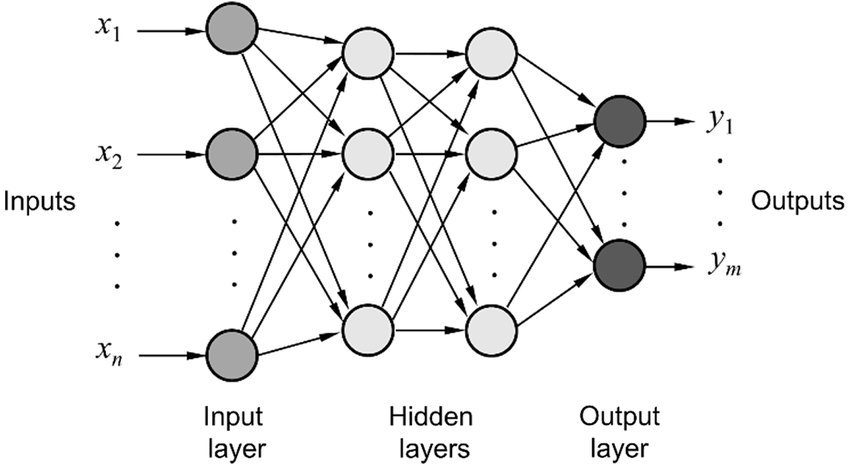
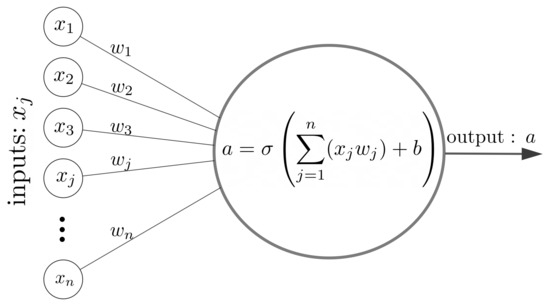
Hãy xem ví dụ về một neural network đơn giản, nó sẽ khá giống với đồ thị tính toán, chỉ là các phép toán phức tạp với hơn với w, g và các activation function như relu, sigmod, softmax, tanh và số lượng và độ lớn cũng nhiều hơn thôi hehe.

Và các node trong đó thì có cấu tạo như thế này:

Python and Vectorization

Một nguyên tắc khi code Deep learning là cần phải vector hóa (vectorization) dữ liệu, bởi vì với những thuật toán trình bày ở trên nếu chúng ta chỉ chạy for đơn thuần thì độ phức tạp thuật toán rất lớn (đâu đó 4 vòng for lồng nhau) vậy nên ma trận và vector sinh ra để giải quyết điều này.

Nếu xếp chồng tất cả m sample của x thì chúng ta có một ma trận đầu vào X với mỗi cột biểu thị một sample (điểm dữ liệu). Vì vậy, bằng cách vector hóa dựng sẵn của numpy, chúng ta có thể đơn giản hóa phép tính gradient descent ở trên bằng một vài dòng mã có thể tăng hiệu quả tính toán một cách chắc chắn.

Z = np.dot(w.T, X) + b
A = sigmoid(Z)
dz = A - Y

Updata parameters:

w = w - alpha * dw
b = b - alpha * db

Tham khảo

Bài viết dựa trên khóa học Deep Learning Specialization Coursera nổi tiếng của Andrew Ng - Link.

Bình luận & thảo luận

Cảm ơn bạn đã dành thời gian để đọc, hãy trò chuyện và góp ý với mình ở dưới hoặc vào bằng link .